
こんにちは!アルファゼミナールです。
数学で学ぶ「フィボナッチ数列」が、実は自然界の中でよく見られることをご存知でしょうか?フィボナッチ数列は、1、1、2、3、5、8、13…といった具合に、前の2つの数を足して次の数が決まるものです。これ自体は数学的な興味から生まれたものですが、この規則性が意外にも自然界の中に頻繁に見られるのです。今回は、フィボナッチ数列が自然界にどのように現れるのか、花びらや貝殻、木の成長など具体的な例を通じて解説します!
フィボナッチ数列とは?

フィボナッチ数列は、13世紀のイタリア人数学者レオナルド・フィボナッチによって紹介されたもので、数列の中で特定のパターンに基づいて進行します。この数列の基本は、2つ前の数字と1つ前の数字を足すと次の数字が得られるというシンプルなルールです。
例:
- 1, 1, 2, 3, 5, 8, 13, 21, 34…
数列が続くほど、前の2つの数字の和がその次の数になるため、順次大きくなっていきます。このシンプルな規則性が、自然界に多くの形で現れています。
フィボナッチ数列と自然界の花びらの数

自然界の植物には、このフィボナッチ数列に基づく規則がしばしば見られます。例えば、花びらの数がフィボナッチ数列に従うことが多いです。具体例を挙げると:
- ユリ:花びらが3枚(フィボナッチ数列の「3」)
- アヤメ:花びらが5枚(「5」)
- ヒマワリ:花びらが21枚(「21」)
なぜ花びらの数がフィボナッチ数列に従うのかについての詳しい理由は、完全には解明されていませんが、植物の成長過程でエネルギー効率やスペースの最適化が関係していると考えられています。
貝殻とフィボナッチ数列の「黄金螺旋」

もう一つの美しい例は、貝殻の形状です。多くの貝殻は、黄金螺旋と呼ばれる曲線を描きながら成長しており、これがフィボナッチ数列と密接に関わっています。黄金螺旋は、フィボナッチ数列の比を無限に拡大すると近似されるもので、この螺旋が貝殻やアンモナイトの成長パターンに見られます。
貝殻がこの形で成長する理由は、スペースを効率的に使うためです。螺旋の形状は、成長するにつれて外部に向かって拡大するため、貝が自身を守りながら効率的に成長できる形とされています。
フィボナッチ数列と植物の成長パターン
また、植物の茎や葉の配置にもフィボナッチ数列の影響が見られます。これは「フィロタクシス」と呼ばれる現象で、植物が成長する際に葉や枝が螺旋状に配置されることで、光や水分の取り入れを最大限にするための効率化が図られています。
例えば、ヒマワリの種の配置や、松ぼっくりの鱗片の螺旋配置も、フィボナッチ数列に基づいた形状をしています。こうすることで、スペースを無駄なく使い、外的要因に対しても効率的に成長できるとされています。
フィボナッチ数列と黄金比の関係
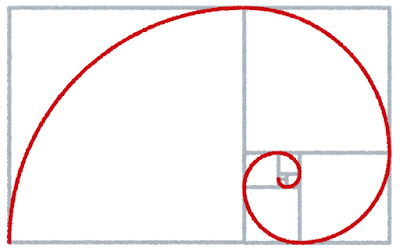
フィボナッチ数列を説明する際によく登場するのが、「黄金比」です。フィボナッチ数列の隣り合う数字の比率は、数列が進むほどに1:1.618に近づきます。この比率は「黄金比」と呼ばれ、古代から建築や芸術において美しいバランスとして知られています。
- パルテノン神殿やピラミッドなど、多くの建築物でもこの黄金比が使われており、自然界だけでなく人間の美的感覚にも影響を与えていると言われています。
まとめ:自然界に隠された数学の神秘
フィボナッチ数列は単なる数学的なパターンに留まらず、自然界のあらゆる場所でその美しい法則性を示しています。花びらの数、貝殻の螺旋、植物の成長パターンなど、これらの例は、自然界が効率的かつ美しく機能していることを示す証拠です。次に自然を観察する際には、フィボナッチ数列の影響を感じ取り、数の神秘に思いを馳せてみてください。では!
この記事を書いた人
アルファゼミナール K.T