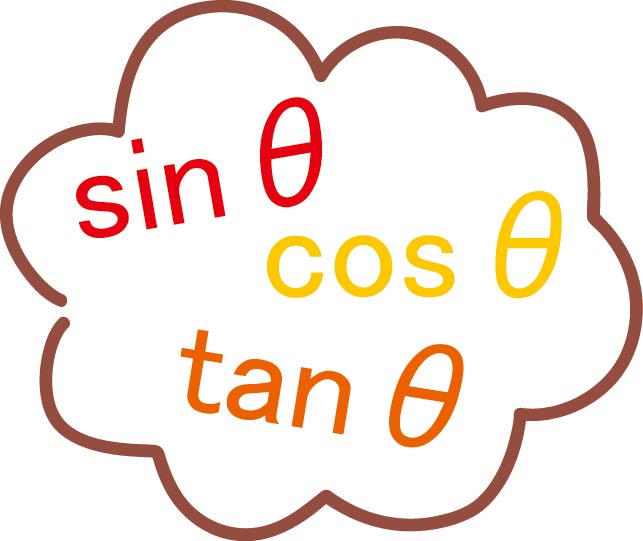
こんにちは!アルファゼミナールです。
高校で習う、数学の中でも特に魅力的な分野の一つである三角関数について、皆さんはどれくらい知っていますか?今回は、三角関数の基本的な定義からその歴史、そして現代の日常生活にどのように利用されているかまでを紹介します。さらに、エジプトのピラミッドとの意外な関係についても触れていきます。
三角関数の公式の説明
三角関数は、サイン(sin)、コサイン(cos)、タンジェント(tan)の三つが基本です。これらは、直角三角形の角度と辺の長さの関係を表します。
- サイン(sin):直角三角形の斜辺に対する対辺の比 sinθ=対辺斜辺\sin \theta = \frac{対辺}{斜辺}
- コサイン(cos):直角三角形の斜辺に対する隣辺の比 cosθ=隣辺斜辺\cos \theta = \frac{隣辺}{斜辺}
- タンジェント(tan):隣辺に対する対辺の比 tanθ=対辺隣辺\tan \theta = \frac{対辺}{隣辺}
これらの関数は、三角形の角度を基に辺の長さを計算するために用いられます。また、これらの関数は周期的な特性を持ち、波や振動を表すためにも広く利用されています。
三角関数の歴史的背景
三角関数は、古代文明にまで遡る歴史を持っています。特に、天文学や航海術の発展において重要な役割を果たしました。
古代ギリシャ 古代ギリシャの数学者ヒッパルコスは、三角関数の基礎を築いた人物とされています。彼は、三角関数を用いて星の位置を計算する方法を開発しました。また、プトレマイオスも天文学において三角関数を利用し、「アルマゲスト」という著書でその知識を体系化しました。
中世イスラム世界 イスラム世界の数学者たちも、三角関数の発展に貢献しました。例えば、アル・ハワリズミは、コサインとサインの関数を用いた天文学の計算方法を記述しました。これにより、天文学の精度が飛躍的に向上しました。
近世ヨーロッパ ルネサンス期のヨーロッパでは、三角関数が航海術において欠かせないものとなりました。船の位置を正確に計算するためには、三角関数を利用した天測航法が不可欠だったのです。
現代の技術における三角関数の利用
三角関数は、現代の様々な技術においても重要な役割を果たしています。以下に、その具体例をいくつか紹介します。
GPS GPS(Global Positioning System)は、衛星からの信号を利用して地球上の位置を計算するシステムです。ここで、三角関数が大いに活用されています。衛星と受信機の間の距離を計算するために、三角関数の公式が利用されます。
音波 音波は波として伝わりますが、その波の性質を理解するためには三角関数が必要です。例えば、サイン波やコサイン波は、音の周波数や振幅を表現するのに用いられます。音楽や音響工学の分野でも、三角関数は不可欠です。
電子機器 電子機器の設計においても、三角関数は重要です。例えば、交流電流の解析や、信号処理、画像処理において三角関数が利用されます。スマートフォンやテレビなど、私たちの日常生活に欠かせないデバイスも、三角関数によって支えられています。
雑学:エジプトのピラミッドと三角関数の関係

エジプトのピラミッドと三角関数には、意外な関係があります。特に有名なのは、ギザの大ピラミッドです。このピラミッドの設計には、三角関数の概念が応用されていると考えられています。
ピラミッドの勾配 ギザの大ピラミッドの高さと基底部の長さの比は、非常に特別な数値に近いとされています。この比は約1.618、つまり黄金比に近い値です。また、ピラミッドの斜面の角度は約52度で、これは tanθ\tan \theta を用いると、非常に美しい数値となります。
数学と建築 古代エジプトの建築家たちは、正確な測量と設計を行うために、三角関数の基本的な概念を理解していた可能性があります。これにより、ピラミッドの安定性と美しさが両立されていたのです。
まとめ
三角関数は、古代から現代に至るまで、数学や科学技術の発展に欠かせない役割を果たしてきました。サイン、コサイン、タンジェントの基本的な定義から、その歴史的背景、現代技術への応用、そして意外な雑学まで、三角関数の魅力は尽きません。これからも、数学の魔法である三角関数を活用して、新しい発見や技術の発展に寄与していくことでしょう。
この記事を書いた人
アルファゼミナール K.T