こんにちは!アルファゼミナールです。
数学の中でも特に美しいとされる「黄金比」についてご存知でしょうか?黄金比は、自然界や芸術、建築など様々な分野で見られる比率で、その美しさと調和の取れた形から古代から現代まで多くの人々に愛されています。この記事では、黄金比の歴史、その導出方法、そして現代における応用例について詳しく解説します。
黄金比とは何か?
まず、黄金比(Golden Ratio)とは何かを説明しましょう。黄金比は、およそ1:1.618の比率を持つ特別な数値関係です。この比率は、数式で表すと次のようになります。
(a + b) / a = a / b
ここで、aとbはそれぞれ異なる長さの線分です。この関係を満たす比率が黄金比です。具体的には、黄金比は無理数であり、その近似値は約1.6180339887です。
黄金比の歴史

黄金比は古代ギリシャで「黄金分割」として知られており、数学者たちの間で広く研究されていました。特に、古代ギリシャの数学者エウクレイデス(ユークリッド)がその美しさと調和を認識し、「原論」において詳述しました。また、古代エジプトのピラミッドやギリシャのパルテノン神殿など、歴史的な建造物にも黄金比が取り入れられています。
フィボナッチ数列と黄金比
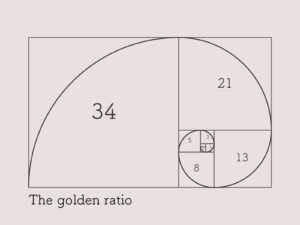
黄金比はフィボナッチ数列とも深く関連しています。フィボナッチ数列とは、1, 1, 2, 3, 5, 8, 13, 21, …というように、前の2つの数を足して次の数を作る数列です。この数列の各項を次の項で割ると、その比は次第に黄金比に近づいていきます。この関係性から、フィボナッチ数列は黄金比の近似として多くの自然現象や芸術作品に現れます。
黄金比の応用例
黄金比は、その美しさと調和の取れた形から、様々な分野で応用されています。以下にその一部を紹介します。
建築: 黄金比は、建築物の設計において美しさとバランスを保つためによく使われます。例えば、パルテノン神殿やル・コルビュジエの建築作品などに黄金比が取り入れられています。
芸術: レオナルド・ダ・ヴィンチやサルバドール・ダリなど、多くの著名な芸術家たちが黄金比を作品に取り入れています。モナリザや最後の晩餐といった有名な絵画にも黄金比が見られます。
自然界: 自然界にも黄金比は多く見られます。例えば、ヒマワリの種の配置、貝殻の螺旋、パイナップルのうろこなど、多くの自然現象が黄金比に従っています。
デザイン: グラフィックデザインやプロダクトデザインでも、黄金比が美しいレイアウトやバランスを作り出すために利用されています。例えば、ウェブデザインやロゴデザインなどで黄金比を取り入れることで、視覚的に魅力的なデザインが実現します。
音楽: 音楽理論においても、黄金比が用いられています。作曲家たちは、楽曲の構成やフレーズの長さに黄金比を取り入れることで、調和の取れた美しい音楽を作り出しています。
黄金比の導出方法
黄金比の値は、以下のようにして導出することができます。
- 黄金比の定義:
- (a + b) / a = a / b
- 数式に変換:
- この関係を満たす数を求めるため、a = 1と仮定し、b = xとします。
- 代入:
- (1 + x) / 1 = 1 / x
- 方程式を解く:
- 1 + x = 1 / x
- x² + x – 1 = 0
- 二次方程式の解の公式を使う:
- x = (-b ± √(b² – 4ac)) / 2a
- x = (-1 ± √(1 + 4)) / 2
- x = (-1 ± √5) / 2
- 黄金比を求める:
- x = (1 + √5) / 2 ≈ 1.6180339887
このようにして、黄金比の値が得られます。
結論
黄金比は、数学の中でも特に美しいとされる比率であり、その歴史や応用を理解することで、数学の魅力を再認識することができます。建築、芸術、自然界、デザイン、音楽など様々な分野で黄金比がどのように使われているかを学ぶことで、数学の実用性と美しさを感じることができるでしょう。この記事を通じて、黄金比の驚くべき応用例を知り、数学の学習をより深めていきましょう。
では!
FAQs
黄金比とは何ですか? 黄金比とは、およそ1:1.618の比率を持つ特別な数値関係で、美しさと調和を保つ比率として古代から現代まで多くの分野で利用されています。
黄金比の歴史はどのようなものですか? 黄金比は古代ギリシャの数学者エウクレイデスが「原論」において記述し、エジプトのピラミッドやギリシャのパルテノン神殿など歴史的建造物にも取り入れられました。
フィボナッチ数列と黄金比の関係は? フィボナッチ数列の各項を次の項で割ると、その比は次第に黄金比に近づきます。この関係性から、フィボナッチ数列は黄金比の近似として自然現象や芸術作品に現れます。
黄金比の具体的な応用例は何ですか? 建築、芸術、自然界、デザイン、音楽など多くの分野で黄金比が応用されています。パルテノン神殿やモナリザ、ヒマワリの種の配置などが例として挙げられます。
黄金比の値はどうやって求めるのですか? 黄金比は、二次方程式を解くことで求められます。具体的には、(a + b) / a = a / bの関係を満たす数を求めると、x = (1 + √5) / 2 ≈ 1.6180339887となります。
なぜ黄金比は重要ですか? 黄金比は、美しさと調和の象徴とされ、建築や芸術、自然界など様々な分野でその美しさとバランスが認められています。そのため、多くの分野で応用され、研究されています。
この記事を書いた人
アルファゼミナール K.T